

| 07-06-2014 (5632 ) | Categoria: Science |
La llei de Chapman-Kolmogorov es basa en l'equació del mateix nom, a la qual van arribar de forma independent el matemàtic britànic Sydney Chapman i el matemàtic rus Andrei Kolmogórov. Enunciada de forma planera diu que "la probabilitat que dos fets que es deuen a l'atzar (i que compleixen unes determinades condicions) s'esdevinguin simultàniament (...) és molt petita".
El concepte era conegut d'antuvi i s'emprava en la investigació forense. Però avui és conegut de tothom que si en un incendi forestal, per exemple, hi ha un sol focus pot ser accidental, però si n'hi ha dos, la probabilitat que sigui provocat és altíssima.
Dins l'entorn d'entrada de dades de les màquines de BULL [1] (amb targetes perforades de tipus Hollerith), es feia una segona entrada de dades llegint alhora les targetes perforades en la primera entrada, i la màquina avisava si hi havia alguna diferència; en cas contrari, es donava com a correcta. D'aquesta manera, la probabilitat d'error passava a ser ínfima.
En tots dos exemples s'està aplicant la llei de Chapman-Kolmogórov, encara que no s'expliciti.
En matemàtiques, concretament en la teoria de probabilitats i, en particular, en la teoria de processos estocàstics markovians, l'equació de Chapman-Kolmogórov és una identitat sobre les distribucions de probabilitat conjunta dels diferents conjunts de coordenades d'un procés estocàstic.
Suposant que {Xi} sigui una col·lecció indexada de variables aleatòries -és a dir, un procés estocàstic- i fent que  sigui la funció conjunta de densitat de probabilitat dels valors de les variables aleatòries X1 a Xn, llavors l'equació de Chapman-Kolmogórov és
sigui la funció conjunta de densitat de probabilitat dels valors de les variables aleatòries X1 a Xn, llavors l'equació de Chapman-Kolmogórov és
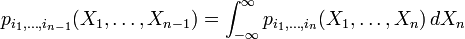
És a dir, una distribució marginal directa sobre la variable destorb.
Cal esmentar que no s'ha assumit res sobre l'ordre de les variables aleatòries, l'equació anterior s'aplica igualment a la distribució marginal de qualsevol d'aquestes variables.
Quan el procés estocàstic objecte d'estudi és markovià, l'equació de Chapman-Kolmogórov és equivalent a una identitat en les densitats de transició. En establir la cadena de Markov, se suposa que i1 < ... < in.
Així, per raó de la propietat de Markov, 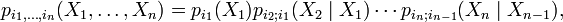 , on la probabilitat condicional
, on la probabilitat condicional 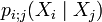 és la probabilitat de transició entre els moments
és la probabilitat de transició entre els moments 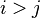 .
.
Així, l'equació de Chapman-Kolmogórov pren la forma 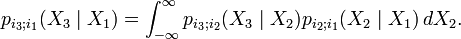
Quan la distribució de probabilitat sobre l'espai d'estats d'una cadena de Markov és discreta i la cadena de Markov és homogènia, les equacions de Chapman-Kolmogórov es poden expressar en termes de producte de matrius (possiblement de dimensió infinita), així:
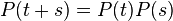
on P(t) és la matriu de transició, és a dir, si Xt és l'estat del procés en el moment t, llavors per a dos punts qualssevol i i j en l'espai dels estats, es té
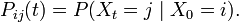
Afegeix-hi un comentari: